The Cornu spiral arises from plotting the two Fresnel integrals against each other. It's a nice, simple spiral that winds up tightly at each end:
As any calculus student can tell you, integration is not a trivial task and the Fresnel integrals are no exception. They don't have a nice analytical form, like, say the integral of 3x2 = x3 + C. Instead, they are evaluated numerically. Generally, computers do this sort of thing quite well, but there are always pitfalls awaiting the naive numerical analyst. Integration typically proceeds by computing a function, marching ahead a step, computing a new value, and repeating until the desired answer is obtained. With the Fresnel integrals and the Cornu spiral, the answer depends greatly on how many steps and how big they are. Here are four different version of the right half of the spiral, each with a slightly different number of steps taken in the integration. Note that all four versions begin together (at the central black dot), but then take off in their own directions. Whereas the correct spiral has only one point (on the right half) about which the spiral winds, each of the approximations stops at a point, winds in, then winds out to moves on to another point.
More fun can be had by tweaking the formulas to be integrated. The correct version works on the functions sin(θ2) and cos(θ2), where θ represents an angle. Why not use other powers of θ? Here's what can happen with exponent values that are close to, but not quite, 2:
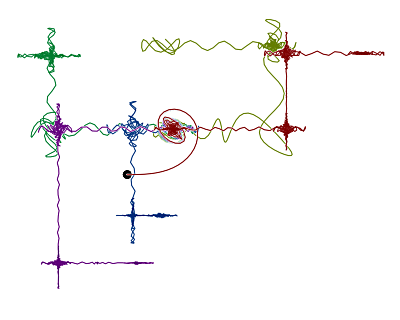Each curve uses a different pair of exponents (say, 1.99 for sin and 2.01 for cos). The curves again start out together, but then take off individually and now don't even maintain the same shape as the original spiral. For even more fun, try different integration methods. Here, I used the trapezoidal rule, but you can find different variations by using the midpoint rule or Simpson's rule, or even combinations of the three.
These are the basic techniques that I used in my images Green Belt and Chocolate City.
As any calculus student can tell you, integration is not a trivial task and the Fresnel integrals are no exception. They don't have a nice analytical form, like, say the integral of 3x2 = x3 + C. Instead, they are evaluated numerically. Generally, computers do this sort of thing quite well, but there are always pitfalls awaiting the naive numerical analyst. Integration typically proceeds by computing a function, marching ahead a step, computing a new value, and repeating until the desired answer is obtained. With the Fresnel integrals and the Cornu spiral, the answer depends greatly on how many steps and how big they are. Here are four different version of the right half of the spiral, each with a slightly different number of steps taken in the integration. Note that all four versions begin together (at the central black dot), but then take off in their own directions. Whereas the correct spiral has only one point (on the right half) about which the spiral winds, each of the approximations stops at a point, winds in, then winds out to moves on to another point.More fun can be had by tweaking the formulas to be integrated. The correct version works on the functions sin(θ2) and cos(θ2), where θ represents an angle. Why not use other powers of θ? Here's what can happen with exponent values that are close to, but not quite, 2:Each curve uses a different pair of exponents (say, 1.99 for sin and 2.01 for cos). The curves again start out together, but then take off individually and now don't even maintain the same shape as the original spiral. For even more fun, try different integration methods. Here, I used the trapezoidal rule, but you can find different variations by using the midpoint rule or Simpson's rule, or even combinations of the three.These are the basic techniques that I used in my images Green Belt and Chocolate City.