As everyone knows, Romeo and Juliett aren’t two star-crossed lovers, they are two of the code words in the NATO phonetic alphabet, or, more accurately, the International Radiotelephony Spelling Alphabet. This is the spoken-word alphabet used by pilots, the military, and others who need to speak over radios and wish to minimize confusion due to similarly-sounding letters. For example, instead of speaking the letters "m" or "n," the speaker would use the code words "mike" and "november," respectively. The alphabet has a different-sounding word for each letter, from a-z:
Romeo and Juliett are the words for the letters r and j, respectively.
Imagine an admittedly silly radio conversation. The sender wishes to communicate the letter "r." She knows to use the phonetic alphabet and says, "romeo." The receiver, not being too smart, asks for clarification. So, the sender tries again. After several botched communication attempts, the sender loses sight of her original desire and fixates on communicating "romeo." So, she spells it: "romeo, oscar, mike, echo, oscar." Several more lacks of understanding, so she tries spelling the spelling words: "romeo, oscar, mike, echo, oscar, oscar, sierra, charlie, alfa, romeo," etc.
At this point, we have all the fixin’s for a string-replacement sequence, so we’ll turn from radio communication to math. A string replacement sequence is one built up in stages: at each subsequent stage, characters from the previous are replaced with given strings. Examples are the Thue-Morse sequence and the Fibonacci word. In this case, we start with the letter r. At each stage, every letter is replaced with its phonetic alphabet code word. The first few stages are:
A couple of things are apparent immediately. First, the sequence of words grows pretty fast. Each subsequent stage has about five times the number of letters as does the previous stage. The 12th stage is almost 200 million letters long!
Second, the beginning of each subsequent stage is just the entirety of the previous stage. This means that, when taken to the infinity stage, the resulting sequence of words is a self-referential fractal sequence. It is self-referential in that it spells itself. That is, if you were to spell each word, in order, using the phonetic alphabet, the result would be the same as reading the list. This follows from how the sequence was created in the first place, by replacing each letter with its respective code word. The fractal nature of the sequence means that the infinite sequence contains infinite copies of itself. One way to see this is by reversing the creation process—replace each word with its first letter and you recover the sequence. Alternatively, list the sequence in a column, each word below its predecessor. Start with “romeo” and highlight it. It has five letters, so count down five words and highlight “oscar” (it’s the third occurrence). Count down five more words for the five letters in “oscar” to “mike” and highlight it. Four more words (for the four letters in “mike”) to “echo,” and then four more words to another “oscar.” The highlighted words are the original sequence. In concept (with an infinite sequence), you could delete the non-highlighted words and repeat this process forever, always coming back to the same sequence.
And what does all this have to do with the image at the top of this post? For either sequence (or for any of the other 24), each letter can be replaced with a number from 1 (for "a") to 26 (for "z"). These numbers can then be used to create images. To see how, look at the picture below. Imagine that you’re at the “start” point and getting ready to draw a line off to the right. Instead, you turn left 45 degrees and draw a line one unit long. Then, turn left again by 45 degrees and draw another line. Repeat this six more times and you’ll have the red octagon.
Increase the turn angle to 60 degrees and you’ll get the hexagon. The other shapes come from turning left 72, 90, and 120 degrees, respectively, before drawing the line. And the star at the bottom comes from turning right 144 degrees before drawing. The point is that, this process of turning a set amount and then drawing a line can lead to many different images.
For “Romeo,” at the top of this page, the turn was about 179 degrees left (almost straight back on itself) for each of 100,000 steps. However, the lengths of the lines varied. Each segment was from 1 to 26 units long, depending on the corresponding letter in the romeo sequence. That is, the first segment was 18 units long, as r is the 18th letter. Below is “Juliett.”
Here, each segment is the same length, but the amount of turning varies. Each turn is about 179 degrees multiplied by the number for the letter in the juliett sequence.
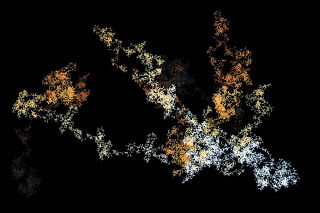
These last two images, “Romeo and Juliett I” and “Romeo and Juliett II,” use both sequences in determining the amount to turn and the lengths of the segments.
| Letter | Word | Letter | Word |
| a | alfa | n | november |
| b | bravo | o | oscar |
| c | charlie | p | papa |
| d | delta | q | quebec |
| e | echo | r | romeo |
| f | foxtrot | s | sierra |
| g | golf | t | tango |
| h | hotel | u | uniform |
| i | india | v | victor |
| j | juliett | w | whiskey |
| k | kilo | x | xray |
| l | lima | y | yankee |
| m | mike | z | zulu |
Romeo and Juliett are the words for the letters r and j, respectively.
Imagine an admittedly silly radio conversation. The sender wishes to communicate the letter "r." She knows to use the phonetic alphabet and says, "romeo." The receiver, not being too smart, asks for clarification. So, the sender tries again. After several botched communication attempts, the sender loses sight of her original desire and fixates on communicating "romeo." So, she spells it: "romeo, oscar, mike, echo, oscar." Several more lacks of understanding, so she tries spelling the spelling words: "romeo, oscar, mike, echo, oscar, oscar, sierra, charlie, alfa, romeo," etc.
At this point, we have all the fixin’s for a string-replacement sequence, so we’ll turn from radio communication to math. A string replacement sequence is one built up in stages: at each subsequent stage, characters from the previous are replaced with given strings. Examples are the Thue-Morse sequence and the Fibonacci word. In this case, we start with the letter r. At each stage, every letter is replaced with its phonetic alphabet code word. The first few stages are:
- romeo
- romeo oscar mike echo oscar
- romeo oscar mike echo oscar oscar sierra charlie alfa romeo mike india kilo echo echo charlie hotel oscar oscar sierra charlie alfa romeo
A couple of things are apparent immediately. First, the sequence of words grows pretty fast. Each subsequent stage has about five times the number of letters as does the previous stage. The 12th stage is almost 200 million letters long!
Second, the beginning of each subsequent stage is just the entirety of the previous stage. This means that, when taken to the infinity stage, the resulting sequence of words is a self-referential fractal sequence. It is self-referential in that it spells itself. That is, if you were to spell each word, in order, using the phonetic alphabet, the result would be the same as reading the list. This follows from how the sequence was created in the first place, by replacing each letter with its respective code word. The fractal nature of the sequence means that the infinite sequence contains infinite copies of itself. One way to see this is by reversing the creation process—replace each word with its first letter and you recover the sequence. Alternatively, list the sequence in a column, each word below its predecessor. Start with “romeo” and highlight it. It has five letters, so count down five words and highlight “oscar” (it’s the third occurrence). Count down five more words for the five letters in “oscar” to “mike” and highlight it. Four more words (for the four letters in “mike”) to “echo,” and then four more words to another “oscar.” The highlighted words are the original sequence. In concept (with an infinite sequence), you could delete the non-highlighted words and repeat this process forever, always coming back to the same sequence.
- romeo
- oscar
- mike
- echo
- oscar
- oscar
- sierra
- charlie
- alfa
- romeo
- mike
- india
- kilo
- echo
- echo
- charlie
- hotel
- oscar
- oscar
- sierra
- charlie
- alfa
- romeo
- …
And what does all this have to do with the image at the top of this post? For either sequence (or for any of the other 24), each letter can be replaced with a number from 1 (for "a") to 26 (for "z"). These numbers can then be used to create images. To see how, look at the picture below. Imagine that you’re at the “start” point and getting ready to draw a line off to the right. Instead, you turn left 45 degrees and draw a line one unit long. Then, turn left again by 45 degrees and draw another line. Repeat this six more times and you’ll have the red octagon.
Increase the turn angle to 60 degrees and you’ll get the hexagon. The other shapes come from turning left 72, 90, and 120 degrees, respectively, before drawing the line. And the star at the bottom comes from turning right 144 degrees before drawing. The point is that, this process of turning a set amount and then drawing a line can lead to many different images.
For “Romeo,” at the top of this page, the turn was about 179 degrees left (almost straight back on itself) for each of 100,000 steps. However, the lengths of the lines varied. Each segment was from 1 to 26 units long, depending on the corresponding letter in the romeo sequence. That is, the first segment was 18 units long, as r is the 18th letter. Below is “Juliett.”
Here, each segment is the same length, but the amount of turning varies. Each turn is about 179 degrees multiplied by the number for the letter in the juliett sequence.
These last two images, “Romeo and Juliett I” and “Romeo and Juliett II,” use both sequences in determining the amount to turn and the lengths of the segments.
Romeo and Juliett I
Romeo and Juliett II